








 sobre 7 comentarios.
sobre 7 comentarios.
SubSet Sum Machine
SubSet Sum Machine
No, expectante lector, como es de suponer, este artículo no te permitirá resolver de forma eficiente los problemas más difíciles de la computación desde hace cientos de años (la computación no existe desde hace cientos de años, pero algunos de sus problemas sí). Sin embargo, espera mostrarte otro punto de vista sobre dichos problemas y ver, cómo puede ser resuelto con una simple fotocopiadora y unas transparencias.
En cuanto al nombre, bueno, en castellano suena un poco mal "máquina del subconjunto suma".
Algoritmo y ordenadores "convencionales"
Los ordenadores pueden realizar determinadas operaciones. Para cualquier problema que queramos que éstos resuelvan, deberá definirse el conjunto de esas operaciones que el ordenador debe realizar para alcanzar la solución al problema, a dicho conjunto de operaciones se le llama "algoritmo".
Algoritmos ¿irresolubles?
Para muchos problemas, se conoce un algoritmo con el cual los ordenadores lo pueden resolver en un tiempo razonable. Sin embargo, existe una serie de problemas cuya solución se les escapa a las más privilegiadas mentes de todos los tiempos y no por nada se les llama "problemas difíciles".
Dentro de este conjunto de problemas difíciles existe un subconjunto que contiene los problemas más difíciles de todos ellos (los que "sólo" son difíciles suelen tener aproximaciones eficientes y razonables), a estos problemas "superdifíciles" se les llama también "completos" (NP-complete).
Si alguien fuera capaz de resolver de forma eficiente uno cualquiera de entre todos los problemas NP-complete, entonces, de forma inmediata, sería capaz de resolver todos y cada uno de los problemas difíciles (incluso cualquiera de los superdifíciles).
Existe una múltitud de fantásticas aplicaciones que podrían realizarse si se pudieran resolver estos problemas (por ejemplo que los ordenadores nos entendieran cuando les hablamos [ojo, los ordenadores sólo saben reconocer la voz, no entienden lo que decimos]).
Personas extremadamente inteligentes piensan que no es posible resolver (al menos de forma "tradicional") este tipo de problemas. Es por ello que deben buscarse formas diferentes de resolver problemas que no sean los tradicionales ordenadores.
El problema "SubSet sum"
Como hemos dicho, resolver uno cualquiera de estos problemas supone resolverlos todos, por ésto, he elegido el problema Subset Sum que, siendo NP-completo, es fácilmente reconocible por cualquier persona (aunque no le gusten las matemáticas). Un enunciado fácil de entender de este problema podría ser el siguiente:
"Si te doy un conjunto de monedas de diferentes valores (de 1, de 2, de 5, de 9, ...). ¿Serías capaz de darme un subconjunto de esas monedas cuya suma sea exactamente la mitad de todas las que te he dado?, y más fácil, ¿podrías decirme tan sólo si prodrías o no dármelas?"
El problema no parece difícil, sin embargo, no se conoce mejor solución que ir revisando todas las posibles combinaciones hasta ver si alguna de ellas suma la cantidad buscada (en realidad existen algunas optimizaciones, pero básicamente el procedimiento sigue siendo explorar todas las posibilidades).
Los mejores algoritmos encontrados que resuelven este tipo de problemas suponen un coste computacional O(2x) lo que quiere decir que, aunque el tamaño del problema crezca sólo un poquito, el tiempo que debe emplear un ordenador crece muchísimo. Se dice que tienen un coste exponencial.
Resolviendo "SubSet sum"
El procedimiento "bruto" para resolver un problema "SubSet sum" es sencillo:
- Se suman todos los números y se divide por dos. A esta cantidad la llamamos Z, y es el valor que buscamos.
- En una libreta, iremos anotando números, si en algún momento anotamos el número Z habremos terminado y responderemos que SI podemos.
- El primer número que anotamos es el 0 (si Z es cero, entonces el subconjunto buscado es el conjunto vacío).
- Para cada número (moneda) que nos han dado, anotaremos las suma de éste número con cada número que ya esté en la lista.
- Si no nos quedan más números, entonces respondemos NO podemos.
Fácil ¿no?. Veamos un ejemplo de su ejecución:
Sean los números { 1, 2, 5, 9, 13 }, entonces tenemos que Z = 15 y haríamos:
| Iteración | Números que quedan | Libreta |
|---|---|---|
| 1 | { 1, 2, 5, 9, 13 } | { 0 } |
| 2 | { 2, 5, 9, 13 } | { 0, 1 } |
| 3 | { 5, 9, 13 } | { 0, 1, 2, 3 } |
| 4 | { 9, 13 } | { 0, 1, 2, 3, 5, 6, 7, 8 } |
| 5 | { 13 } | { 0, 1, 2, 3, 5, 6, 7, 8, 9, 10, 11, 12, 14, 15, 16, 17 } |
El procedimiento es muy sencillo y fácil de hacer para un ordenador, sin embargo ¿porqué no es eficiente?. Bueno, si nos damos cuenta, para cada número que sacamos de la lista original, los números en nuestra libreta se multiplican por dos, lo que significa que si nos dan 4 monedas, anotaremos hasta 24=16 números en la libreta, si nos dan el doble de números tendremos que anotar 28=256 números ¡16 veces más!. Pero es que si nos dan tan sólo 50 monedas, tendremos que anotar nada menos que 1.125.899.906.842.624 números. Teniendo en cuenta que para resolver problemas prácticos nos darán algunos miles de monedas, es obvio que el procedimiento no es útil.
Del método anterior vemos que no hay problema en ir consumiendo las monedas que nos dan una a una. Si nos dan 10 monedas, tendremos que hacer el trabajo 10 veces, si nos dan 100 lo haremos 100 veces.
Los problemas del método anterior son dos: por un lado, tenemos que anotar una cantidad enorme de números en nuestra libreta, cuando la memoria de los ordenadores es limitada; por otro lado, tenemos que realizar una cantidad gigantesca de operaciones (pues cada número que anotamos supone realizar el doble de sumas). Con sólo 50 monedas, necesitaríamos una memoria de 1 PetaByte (un superordenador realmente) y realizar tantas sumas, que a un procesador de 8 GHz le llevaría más de 3 días ininterrumpidos. Y fíjate que aun teniendo semejante ordenador, con sólo una moneda más ya le costaría el doble de tiempo, con dos monedas más ¡el cuadrúple!...
Si queremos resolver el problema eficientemente, tendremos que conseguir dos cosas, por un lado, almacenar una cantidad enorme de información y por otro, realizar todas las sumas simultáneamente.
La máquina que resuelve "SubSet sum"
Os presento una máquina que ya existe, que es muy común en todo el mundo y que casi cualquier persona la tiene en su propia casa, es la fotocopiadora, nos permitirá realizar todas las sumas en un sólo paso.
Como soporte de almacenamiento, tan sólo necesitamos las tan conocidas (al menos en la universidad) transparencias que almacenarán todos los resultados de las operaciones. Si nos dan 10 monedas, necesitaremos 10 transparencias, si nos dan 100 monedas tan sólo necesitaremos 100 transparencias. Fácil ¿no?, incluso conseguir 1000 transparencias no parece nada complicado.
El algoritmo para resolver "SubSet sum" en nuestra fotocopiadora es sencillo:
- Todas nuestras transparencias deben tener en la base una línea negra horizontal.
- Tomamos la primera transparencia y la ponemos en la fotocopiadora desplazada una longitud linealmente proporcional a la primera moneda.
- Hacemos una fotocopia en una transparencia nueva.
- Sin quitar la primera transparencia, ponemos la copia realizada desplazándola una longitud linealmente proporcional a nuestra segunda moneda.
- Hacemos una fotocopia en una transparencia nueva.
- Sin quitar ni la primera ni segunda transparencias, ponemos la copia realizada desplazándola una longitud linealmente proporcional a nuestra tercera moneda.
- Y así sucesivamente, repetimos el proceso haciendo tantas copias como monedas nos hayan dado o bien cuando exista una línea horizontal en la posición linealmente proporcional al valor Z buscado.
El método es tan simple que apenas requiere de explicación. Cada fotocopia que realizamos contiene todos los números anteriores y al desplazarla, estamos sumando todos esos números al del desplazamiento ¡a la vez!.
¿Dónde está el truco de la máquina que resuelve "SubSet sum"?
No hay truco, los problemas técnicos asociados a la máquina no son tales. Uno puede decir que no es posible hacer una fotocopia cuando en lugar de una hoja tenemos un bloque de (digamos) 30 transparencias, pero este sencillo problema se resuelve haciendo una fotocopia adicional cada pocas (e incluso a cada una) fotocopias "desplazadas". También se puede quejar uno de que no es posible calibrar el desplazamiento que debe hacerse cuando los números son muy grandes (y por tanto el desplazamiento muy pequeño) pero existen elementos para calibrar a nivel atómico. Otros problemas como la dispersión de la luz al atravesar la transparencia son "sólo" problemas técnicos que de una u otra forma podrían resolverse.
Es obvio que la construcción de la "SubSet Sum Machine" distaría de ser la tan sencilla fotocopiadora, sin embargo es notable que podría resolver los mayores tamaños que pueden resolver las más poderosas máquinas de la actualidad en ¡fracciones de segundo! (dicho sea de paso, bien escasos n=30 lo cual no los hace útiles en la práctica).
La limitación real de la máquina consiste exactamente en la misma limitación de los algorítmos "tradicionales", aunque pudieramos calibrar nuestra fotocopiadora a nivel atómico y nuestras transparencias fueran una sucesión de átomos de hidrógeno, "sólo" podríamos disponer en cada hoja de 2.834.500.000 átomos, lo que significa que en una hoja sólo podríamos resolver problemas de hasta 31 monedas (eso sí, lo haríamos mucho más rápido). Pero es que, aunque en lugar de una simple hoja (DIN A4) usáramos la longitud de una gran película de cine (digamos de 100 metros), tras semejante esfuerzo sólo nos daría para 37 monedas ¡sólo 6 más!.
Conclusión
En definitiva, cualquier intento por resolver este tipo de problemas, debe pasar por acotar la explosión combinacional (lo cual aunque no demostrado, parece que es imposible con el famoso P vs. NP) o bien descubrir nuevas relaciones físicas que nos suministren nuevas operaciones (nuevos ordenadores) que permitan almacenar y procesar simultáneamente dichas combinaciones. Muchas personas tienen sus esperanzas puestas en la computación cuántica.
Estaremos atentos.
Opinado el 10/06/10 06:10, valoración










Si el numero dado fuera la constante de un cuadrado magico y existiesen los elementos de -al menos- una fila o columna o diagonal del cuadrado ¿no se le daria soluci?l problema? (o a un caso especial)?. MUY INTERESANTE EL ARTICULO, SALUDOS. Me interesa su opinion sobre lo que anteriormente he planteado
Opinado el 10/06/10 08:47, valoración










Hola, desde el momento que nuestro hipotético cuadrado mágico sólo contendrá el subconjunto solución (y no el resto de números del conjunto inicial) y dado que pueden existir múltiples cuadrados mágicos con una constante mágica dada, no veo la forma de relacionar ambos problemas. Es decir, si hemos construido el cuadrado mágico ¡es porque hemos solucionado previamente el problema Subset sum!. Saludos.
Opinado el 28/12/11 16:28, valoración










aprovecha todo lo que puedas tu gran mente...chao
Opinado el 27/04/13 03:41, valoración










hola
Opinado el 16/01/16 02:59, valoración










https://npnanaloqo.wordpress.com/2016/01/14/22/
Opinado el 13/07/20 19:33, valoración










yo ya realice el algoritmo con 6 variables
Opinado el 15/07/20 13:34, valoración










¿Con 6 variables? claro, eso son 2^6=64 posibles










 Windows Management Instrumentation I
Windows Management Instrumentation I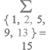 SubSet Sum Machine
SubSet Sum Machine Sobrecarga de operadores
Sobrecarga de operadores Operaciones en coma fija
Operaciones en coma fija Coseno rápido
Coseno rápido Resolver Sokoban
Resolver Sokoban Derivada Simbólica
Derivada Simbólica Camino óptimo
Camino óptimo