








 sobre 8 comentarios.
sobre 8 comentarios.
Coseno rápido
Para qué
Actualmente, la forma más rápida de calcular una función trigonométrica (y otras) es sin duda usar un procesador que soporte este tipo de intrucciones en las operaciones de coma flotante (antaño usando un coprocesador matemático), sin embargo existen varios motivos por los que merezca la pena usar métodos alternativos: la obvia es que quizás no dispongamos de dicha instrucción (p.e. en un teléfono móvil o un microcontrolador), otra es porque estemos operando en coma fija o con enteros y entre la propia función y las operaciones de conversión que deben hacerse, resulta más económico (en tiempo) otras opciones, quizás no necesitemos tanta precisión en cuyo caso también sale más rentable no usar dichas funciones "rápidas" y calcular nosotros directamente el coseno.
Como se calcula el coseno
Gracias a auténticos monstruos como Brook Taylor (1685-1731) o Colin Maclaurin (1698-1746) es trivial realizar el desarrollo en serie de muchas funciones interesantes, estos desarrollos aproximan mediante un polonomio la función, algo muy adecuado para implementar en un ordenador.
Concretamente, el desarrollo en serie de la función coseno es la siguiente:
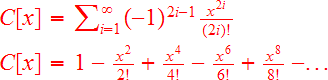
Como lógicamente no vamos a calcular los infinitos términos, lo suyo es saber hasta que término debemos calcular para conseguir una predeterminada precisión, así, si enumeramos los términos como n=2,4,6,..., podemos expresarlos como:
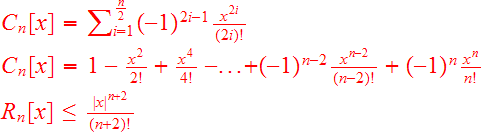
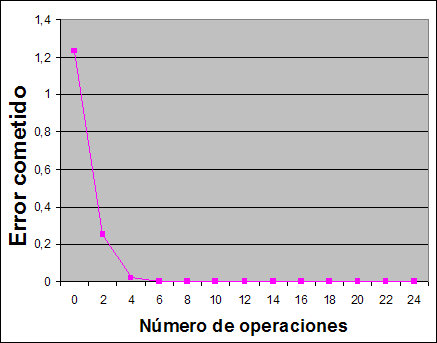
Se aprecia que el rendimiento de la aproximación es tremendo, pues el error cometido respecto de las operaciones realizadas es ¡inversamente factorial! (mucho mejor que exponencial), es decir, incrementando sólo un poco el número de operaciones, incrementamos enormemente la precisión del cálculo.
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
¿Realmente el procesador lo hace rápido?
Es trivial implementar este desarrollo en serie, pero no caigáis en la tentación (soy débil, yo caí...) de intentar agrupar (sacando factor común), pues la pérdida de precisión al convertir la suma de productos en un producto de sumas hace que los errores de redondeo destrocen los resultados.
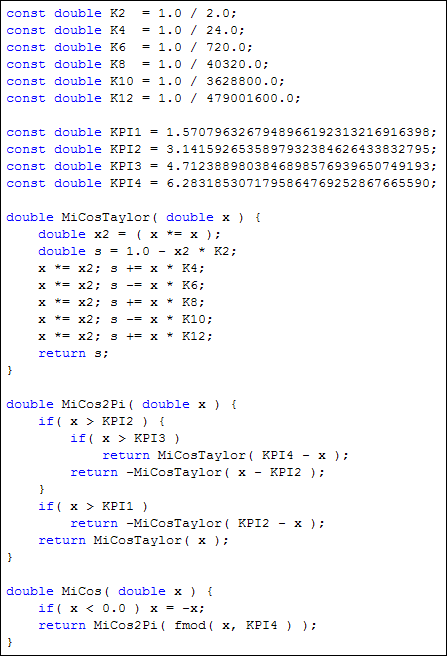
El algoritmo anterior no tiene mucha miga, MiCos se asegura de que los valores sean positivos (la función coseno es simétrica) y obtiene el representante del parámetro entre 0 y 2·Pi; la función MiCos2Pi realiza las transformaciones del 2º, 3º y 4º cuadrantes al 1º y finalmente MiCosTaylor aproxima el valor en el 1º cuadrante.
Según la tabla de acotación del error tendríamos en este caso un error máximo de 6,387e-9 (que no está nada mal), aunque en la práctica (esa cota de error, acota el peor caso, en Pi/2) obtendríamos un error medio de 4,2e-10, teniendo en cuenta también que el rendimiento de dicha implementación iguala (en un AMD Atlhon 64 X2 Dual Core 3800+) a la interna del procesador (que conlleva un fabuloso error medio de 1e-17) podemos decir que la implementación interna está bien, pero que no es para tirar cohetes.
NOTA: el considerar los errores medios no debería estar (en la práctica) permitido, pero si es válido para la teoría si sabemos que la distribución del error en el primer cuadrante nos permitirá reducir en media el número de ciclos, con sólo considerar n diferente para diferentes divisiones del cuadrante.
Más rápido
Normalmente, la forma más rápida de obtener el valor de una función (no trivial) cuando se necesita, es tenerlo ya calculado, el concepto de caché (de disco, de procesador, de servidor de aplicaciones, memoize, etc...) es un buen ejemplo. Normalmente desde el punto de vista del consumo de tiempo suele ser la mejor opción, puesto que el tiempo de recuperar un valor calculado suele ser constante (y si dicho tiempo nos satisface, pues ya está). Para tener disponibles los valores, éstos deben estar en algún tipo de memoria, pero éste es un recurso escaso (si escaso, otra cosa es que nos bastate con la que tenemos... piensa en la memoria de ejecución de que dispone un teléfono móvil o en todos los valores coseno que pueden calcularse y que deberían almacenarse).
De hecho, una de las formas tradicionales de obtener rápidamente el coseno (u otra función trigonométrica) es precalcular éstos en una tabla, lógicamente no todos (son infinitos), sólo aquellos que se necesiten o unos pocos elegidos. Por ejemplo, supongamos que un usuario puede rotar (sobre el plano horizontal) una cámara, y que el control (p.e. un botón) aumenta o disminuye el ángulo de rotación en un grado; en tal caso, bastaría con almacenar 360 valores (de 0 a 359) y el coste del cálculo sería recuperar un valor de la memoria.

De esta forma, se obtiene un rendimiento (respecto de usar el coprocesador) de 20 veces mejor. Sin embargo tiene graves implicaciones: por un lado la precisión está supeditada directamente al número de elementos precalculados y teniendo en cuenta que la mayor pérdida de precisión está en los puntos ( 0, +1 ) y ( 0, -1 ), si se está precalculando toda la esfera unitaria tenemos que el error máximo cometido para N elementos precalculados no supera 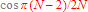 (que podemos aproximar por
(que podemos aproximar por 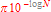 cuando n es grande [a partir de 100]), y por otra parte no podemos usar directamente un acceso a los elementos precalculados, pues su índice es un valor entero en [0, N) y su uso debe realizarse teniendo esto en cuenta en los cálculos, siendo lo más adecuado usar coma fija para evitar conversiones de float, double a int, long y viceversa.
cuando n es grande [a partir de 100]), y por otra parte no podemos usar directamente un acceso a los elementos precalculados, pues su índice es un valor entero en [0, N) y su uso debe realizarse teniendo esto en cuenta en los cálculos, siendo lo más adecuado usar coma fija para evitar conversiones de float, double a int, long y viceversa.
Conclusión: el coseno discreto suministra una mejora constante (no superará nunca un factor de mejora [en nuestro caso de 20]) con un coste muy elevado, tanto de diseño de los algoritmos en los que se use como de la cantidad de memoria a usar en función del error (cuya relación ya vemos que es tristemente lineal).
¿Es mejorable el coseno discreto?
Claro, acceder directamente al valor precalculado (cuyo índice entero se aproxime más) es la opción trivial (y la más óptima), sin embargo aún tenemos margen entre una única instrucción de acceso del coseno discreto y el conjunto de operaciones del cálculo del coseno presentado antes. La siguiente alternativa obvia parece promediar (dos accesos al vector, una suma y una división por dos), la siguiente interpolar (dos accesos al vector, dos restas, dos productos y dos sumas), etc... no obstante este tipo de estrategias sólo hace que la relación de linealidad entre el error cometido y el número de elementos a memorizar sea más favorable a costa de nuestro recursos más preciado, el tiempo.
Opinado el 20/08/09 02:53, valoración










esta muy bueno es practico , gracias
Opinado el 29/04/11 00:21, valoración










Hay una forma mucho más optima de calcular senos, cosenos, exponenciales, trigonometría hiperbólica y logaritmos usando basicamente el mismo algoritmo. Investigálo, se llama cordic!!! Converge a un bit por iteración, lo malo, es en punto fijo
Opinado el 03/05/11 11:11, valoración










Cordic, ¡NO ES mucho más óptimo! (de hecho, es bastante menos óptimo), únicamente se usa cuando sólo se puede sumar y restar. En cuyo caso, probablemente sea mejor alguna de las opciones que comento...
Opinado el 24/01/12 23:19, valoración










Opinado el 01/07/13 10:20, valoración










Muy interesante el "Coseno rápido". Gracias.
Opinado el 11/07/13 05:01, valoración










estubo bakan
Opinado el 19/09/13 04:08, valoración










Genial! me re sirvio, muchas gracias!
Opinado el 23/09/19 02:27, valoración




















 Windows Management Instrumentation I
Windows Management Instrumentation I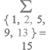 SubSet Sum Machine
SubSet Sum Machine Sobrecarga de operadores
Sobrecarga de operadores Operaciones en coma fija
Operaciones en coma fija Coseno rápido
Coseno rápido Resolver Sokoban
Resolver Sokoban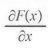 Derivada Simbólica
Derivada Simbólica Camino óptimo
Camino óptimo