Meta balls (2007)

Una de las estructuras más interesantes para generar geometrías por ordenador son las metaballs (meta bolas), pues con una sencilla definición es posible realizar objetos muy interesantes.

Informalmente, una meta bola tiene un comportamiento muy parecido a una gota de agua en un medio sin gravedad. En estas condiciones, una gota sola presentará una forma totalmente esférica; dos gotas próximas que se toquen ligeramente, compartirán un lazo de unión y dos gotas muy próximas estarán cerca de formar una única gran gota.

Diferentes objetos matemáticos pueden utilizarse para definir este tipo de geometrías, de hecho, para ser exactos, el término metaball es sólo una de las diferentes formas de hacerlo. No obstante, el principio es siempre el mismo, y se basa en determinar dentro de un espacio cuatridimensional el subespacio tridimensional que posee una propiedad concreta es decir, es un caso de función implícita (U(X,Y,Z)=k).

Para ser más concretos, supongamos que tenemos cuatro cargas eléctricas situadas en un espacio tridimensional, cada carga produce un campo de energía que es más intenso cuanto más próximo a la carga se encuentre. Tenemos entonces definido un espacio cuatridimensional: el eje X, el eje Y, el eje Z y el eje de intensidad. Para cualquier punto del espacio, podremos medir la intensidad como resultado de sumar las generadas por cada carga. Si nos proponemos determinar el espacio en el que la intensidad es un valor k concreto y fijo, obtendremos un relieve (como en los mapas de nivel) que es precisamente el espacio cuya energía es k (es decir, aquellos X, Y y Z que cumplen que U(X,Y,Z)=k). Exigir niveles altos de energía supondrá que el relieve estará próximo a los centros de las cargas, mientras que exigir niveles bajos de energía supondrá que el relieve englobará múltiples cargas simultáneamente.

Diferentes funciones de energía pueden ser utilizadas, aunque lo más habitual será utilizar una que sea función de la distancia al centro de la carga ( y por tanto esférica).

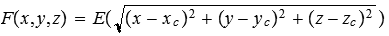
De entre los diferentes métodos para definir la intensidad aportada por una carga a una distancia dada, se destacan:

• Blobby Molecules (moléculas de agua), el aporte de una carga decrece exponencialmente con la distancia. Se atribuye a Jim Blinn, y parece ser la primera forma de representación de este tipo de objetos.
  

  

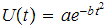
• Meta Balls, se diferencian tres intervalos de distancia, evaluándose ecuaciones de segundo grado en los dos primeros y siendo constante en el tercero (igual a cero).
  

  

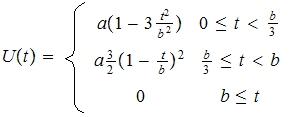
• Soft Objects (objetos suaves), similar a las meta bolas, pero el grado del polinomio es seis y sólo se evalúa en un intervalo (fuera de él es cero), se atribuye a los hermanos Wyvill.
  

  

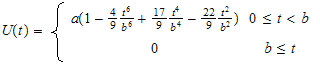
En general parece más atractivo utilizar el último método, pues al ser la distancia entre puntos la raíz cuadrada de la suma de los cuadrados de las distancias en cada componente, la expresión resultante es únicamente un polinomio de hasta grado sexto, pues se elimina la raíz cuadrada y sólo queda determinar las raíces de un polinomio.

No obstante, sólo existen fórmulas explícitas para calcular las raíces de polinomios de hasta cuarto grado, polinomios de mayor grado precisan (en general) de métodos iterativos (bisección, newton, secante, etc...). Si queremos tener la ventaja de eliminar la raíz cuadrada, el polinomio (de sexto grado) a utilizar deberá ser de la forma

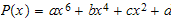
Partiendo del supuesto de tener carga 1 en el orígen y 0 en 1 (de querer tomar otros valores serían sendos cambios de escala, uno sobre cada eje), los coeficientes deben cumplir

• P(0) = 1
• P'(0) = 0
• P(1) = 0
• P'(1) = 0

la segunda ecuación no aporta nada al sistema, por tanto tenemos sólo tres ecuaciones y la solución estará condicionada por el valor de uno de los coeficientes (es decir, hay infinitas soluciones), en cualquier caso, el polinomio nos queda de la siguiente forma

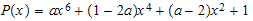
y el parámetro a debe estar entre -1 y 0 para que sus valores determinen una función de energía válida. Si nos fijamos en los diferentes polinomios obtenidos tenemos tres alternativas

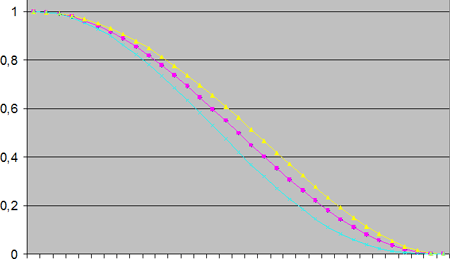
la primera (azul) es para a = -1 y aproxima mejor el tipo de curva que se espera de una función de energía y obtiene los mejores resultados de suavidad cuando se fusionan mútiples cargas; la segunda (rojo) es para a = -4/9 y es la aproximación de los Wyvill (la cual he de suponer que es la preferida al ser la "suavidad" de la curva en 0 y 1 equivalentes, aunque no veo que ventaja se obtiene, pues los valores cercanos al orígen nunca serán elegidos); la tercera (amarillo) es para a = 0 y siendo la menos suave, tiene una gran ventaja respecto a las otras dos, y es que el polinomio se reduce a uno de cuarto grado obteniéndose expresiones explíticas para buscar las raíces (que nos permiten encontrar las "curvas de nivel").

En definitiva, puesto a utilizar un polinomio de estas características yo tomaría la alternativa azul y en caso de querer (necesitar) optimizar el proceso la amarilla.

Renderizado

Si se decide utilizar polinomios para definir la distribución de la energía de cada carga, el alcance de cada una de ellas está acotado por su radio máximo de acción; más allá, su aporte es nulo. Así pues, para cada rayo de visión (se denomina así a los rayos que parten de la cámara u observador e inciden en los objetos a visualizar) habrá que determinar las intersecciones con cada una de las esferas contenedoras. Cada uno de los intervalos existentes entre cada uno de los cortes producidos sobre el rayo de visión, estará incluído en una o varias de las esferas que acotan las cargas y será la función suma de todas estas cargas de la que habrá que buscar las raíces (aquellos valores de frontera para un determinando nivel de energía), de existir una raíz, es que el rayo de visión intersecta con la superfície.

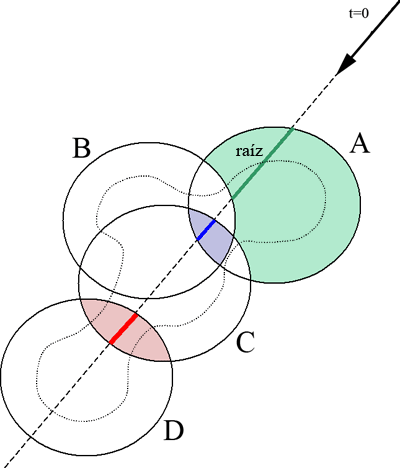
Para un conjunto de N cargas, deben evaluarse N intersecciones (entrada y salida) entre esferas y el rayo de visión y ordenar todas las intersecciones. Para esto, caben básicamente dos alternativas:

• Vector estático y ordenación Qsort, si son conocidas el número de cargas, dimensionamos un vector de 2 N intersecciones y ordenamos por Qsort.
• árbol balanceado, pueden ir procesándose las intersecciones e insertarlas en un árbol balanceado, el árbol resultánte contendrá las intersecciones ordenadas.

En teoría es más eficiente el árbol balanceado, pues tiene un coste de inserción en el peor de los casos O(log n) con lo que tenemos un coste máximo de O(n log n) para obtener la lista de cotas ordenadas. Por contra Qsort nos obliga a añadir los elementos y luego ordenarlos, pero además, el peor caso de Qsort es O(n^2) aunque esto es raro y suele admitirse como válido su promedio que es O(n log n) y tenemos un coste medio total de O(n + n log n).

Así pues aunque teoricamente resulte sensiblemente más eficiente, el árbol balanceado tiene una constante multiplicativa mucho mayor que Qsort y por tanto para tamaños pequeños será mucho más rentable (por ejemplo Qsort sólo requiere un paso de reservar memoria y otro de liberar memoria, el árbol balanceado requiere reservar n bloques de memoria y liberar n bloques de memoria). Para dar cifras que orienten esta decisión, imaginemos una escena con 1.000 millones (es mejor ponerse en un muy mal caso) de pequeñas metabolas (por ejemplo simulando un líquido) distribuidas uniformemente, para cada rayo de visión tendremos entre 1.000 y 1.732 (la diagonal) cargas aproximadamente, un número muy pequeño en la mayoría de los casos que hace que sea mejor un algoritmo con una constante pequeña (pero no sea malo, obviamente).

Existen alternativas que utilicen un árbol balanceado mediante un único vector (recordemos que es conocido el número de elemento máximo a ordenar) que minimizaría en gran medida su constante multiplicativa. De todas formas, no será hasta analizar los tiempos de ejecución de las diferentes partes del programa cuando se vea la necesidad de optimizar una ordenación por Qsort que ni siquiera debemos implementar (es una sencilla función disponible en C).

Cálculo efectivo del polinomio de energía

Hemos acordado que la energía aportada por una carga en un punto q se obtenía por un polinomio P(x) donde x es la distancia del punto q al centro de la carga.

Normalmente al parámetro de las ecuaciones paramétricas que determinan el rayo de visión se le denomina t y coincide con la distancia recorrida (si el vector director está normalizado, claro), por tanto, la energía aportada por una carga i-ésima en cada punto del rayo de visión será Pi( | o + d · t - Ci | ) (siendo o el orígen del rayo de visión, d su vector director y Ci el centro de la carga i-ésima). Si acordamos en utilizar el polinomio de cuarto grado para ahorrarnos procesar una ecuación implícita con una raíz cuadrada, tenemos:

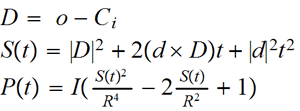
donde la primera ecuación es símplemente el vector diferencia entre el centro de la carga y el orígen del rayo de visión. La segunda es la ecuación de segundo grado que coincide con el cuadrado de la distancia entre cada punto del rayo de visión y el centro de la carga. La tercera ecuación es el resultado de sustituir el cuadrado de la distancia en el polinomio que determina la energía de la carga. Los coeficientes R e I aparecen al realizar el cambio de escala anteriormente mencionado donde el coeficiente I es la intensidad máxima de la carga (en su centro) y el coeficiente R es el radio de la esfera contenedora de la carga (teniendose que en su superfície y exterior la energía de la carga es nula).

Una vez ordenada la lista de las 2 N intersecciones (las de entrada y las de salida), sólo basta ir evaluando los polinomios suma de todas las cargas intervinientes en cada tramo, el proceso sería más o menos así:

• Definimos un polinomio P(x) = -K donde K es la constante del nivel de carga que determina la superfície (de función implícita).
• Recorremos en orden las cotas de intersección ordenadas realizando los pasos:
  • Si el polinomio P tiene raíces en el intervalo actual, tenemos la intersección (en la raíz encontrada).
  • Si la cota es de entrada, sumamos a P el polinomio Pi asociado a la carga de la cota (de entrada).
  • Si la cota es de salida, restamos a P el polinomio Pi asociado a la carga de la cota (de salida).

Cálculo de la normal en el punto de intersección

El punto de intersección es sencillo de calcular, pues la raíz nos indica la distancia recorrida por el rayo de visión, luego el punto de intersección es q = o + d · t.

Ahora bien, para calcular la normal de la superfície en el punto q lo primero que uno piensa es en diferenciar respecto cada coordenada (X, Y y Z) la función implícita (obtenida al combinar las funciones implícitas de cada carga interviniente), sin embargo esto requiere calcular y gestionar 3 funciones reales de 3 variables para cada carga y sus respectivas sumas y restas (al combinarse varias cargas en cada intervalo, de la misma forma que hemos hecho con los polinomios de nivel de energía) y existe una forma mucho más sencilla, puesto que ya tenemos calculado cada polinomio Pi de cada carga y puesto que el parámetro t es conocido y puesto que calcular la normal (no normalizada) son 3 simples restas (q-Ci), sólo debemos evaluar el polinomio Pi de cada carga en t para obtener el nivel de energía en ese punto (para esa carga) y multiplicarlo a la normal (no normalizada) para tener correctamente promediadas las normales de cada carga interviniente. Es decir:

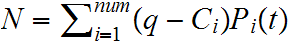
Mezclando colores

De forma similar al promedio de normales, se puede realizar para determinar el color de emisión en el punto de intersección con la superfície, lo único que en lugar de promediar las normales se promedian los colores asociados a cada una de las cargas.

Optimización

Si la idea es trazar cientos de miles de cargas (por ejemplo para simular un líquido), para cada rayo de visión sólo unas pocas (miles, pero pocas si tenemos cientos de miles) tendrán intersección, el cálculo de la intersección del rayo de visión con la esfera que contiene la carga no es costosa, de hecho en 11 sumas y 7 multiplicaciones se determina si tiene intersección o no, no obstante, si tenemos una imágen con una resolución digamos de 1024x758 píxeles (no aplicamos antialiasing) resulta que cada carga debe revisarse 786.432 veces es decir 14.155.776 operaciones (sin contar con las operaciones adicionales de comparación salto de intrucción, etc...) si tenemos "tan sólo" cien mil cargas, supone un total de 1.415.577.600.000 operaciones, resumiendo que a un ordenador con una capacidad de 1 Teraflops le llevaría ¡más de un segundo! y esto sólo la intersección del rayo de visión con las esferas contenedoras de las cargas.

Existen muchas formas de estructurar la información de la escena para optimizar la búsqueda, árboles BSP, Octrees, Bounding-Box, etc... son algunas de las técnicas más utilizadas. Sin embargo, no son triviales de implementar (no es que sean difíciles, en Trazador de rayos puedes bajarte mi implementación, pero se debe perder su tiempo).

Una forma con una constante multiplicativa nula, muy sencilla de implementar y muy adecuada para esta densidad de esferas, es la siguiente, aunque eso sí, tiene un gran inconveniente y es que es dependiente del view port (punto de vista de la cámara) lo que sólo sirve para optimizar los ray-casting emitidos desde la cámara:

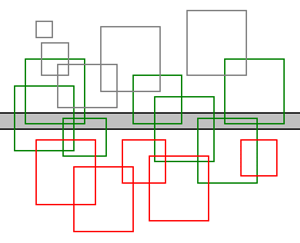
• Para cada carga de entrada, calculamos su caja 2D contenedora en nuestro view-port, insertamos las dos referencias Ymin e Ymax en un árbol balanceado (para que el coste total de creación del árbol sea O(n log n)) con lo que obtenemos una lista ordenada que llamaremos LY con las cotas sobre el eje Y de las cajas acotadoras.
• Mantendremos un árbol balanceado llamado LX inicialmente vacío.
• Para cada avance del scan-line horizontal (es cada línea de píxeles horizontal en la imagen), es decir el avance es de la coordenada Y, procesamos las coordenadas en LY que queden por debajo (normalmente mirando la imagen será "queden por arriba", pues el origen suele estar en la esquina superior izquierda):
  • Si es una cota Ymin añadimos a LX el marco de acotación (sus cotas Xmin y Xmax respectivamente).
  • Si es una cota Ymax sacamos de LX el marco de acotación (y podemos ir borrando si queremos de LY aunque si hemos mantenido el árbol balanceado, lo más óptimo es esperar a terminar para borrar el árbol de los nodos hoja a los nodos raíz con el fin de no tener que hacer rotaciones).
• Una vez realizado el avance, sólo tenemos que ir avanzando sobre LX píxel a píxel y tenemos la sublista con las cargas cuyo marco de acotación tiene intersección no vacía (con cada píxel).

En esta situación, cada carga realmente sólo está presente (en todo el proceso de cálculo) en aquellos píxeles que ocupa su caja de acotación y si hay muchas cargas será porque son pequeñas (no tiene sentido muchas muy grandes) y por tanto pocos píxeles de superfície, en las condiciones de renderizado anteriores, una carga ocupará aproximadamente la 46-aba parte del viewport (si tenemos cien mil cargas, la raíz cúbica es 46) por tanto hemos reducido la constante multiplicativa en 46 veces (que es mucho mejor que mejorar en una proporción lineal de 46 veces), al reducir las comprobaciones a la casi totalidad de las veces que sí se producirá intersección.

Solución inmediata

No obstante, todavía se pueden obtener resultados igual de buenos pero trabajando mucho menos a costa tan sólo de disponer de "un poco" más de memoria.

Si tenemos una imagen como la indicada, podemos definir un vector de 1024x768 listas símplemente enlazadas de cargas. Basta entonces calcular las cajas de acotación e insertar las cargas en las listas de los píxeles que estén dentro. Esto supondrá un coste en memoria bastante elevado, pero con uno 500Mbytes se pueden renderizar hasta 200.000 cargas en unos pocos segundos (1 único procesador AMD Athlon 64). No obstante, aunque en cuanto a la velocidad es una solución óptima, es una bastante mala solución desde el punto de vista de los recursos de memoria.

Cálculo de la caja de acotación

Suponiendo que la carga esté situada delante del plano de proyección de la imagen (lo que viene a ser la pantalla de la televisión), la proyección de la esfera que contiene la carga sobre el plano es (en general) una elipse, si lo pensamos un poco nos daremos cuenta que la elipse proyectada se alarga en la dirección del vector director (proyectado) del rayo que apunta al centro de la carga. Con algo de geometría básica, podemos obtener sin dificultad los puntos extremos de dicha elipse (a lo largo del eje principal), concretamente:

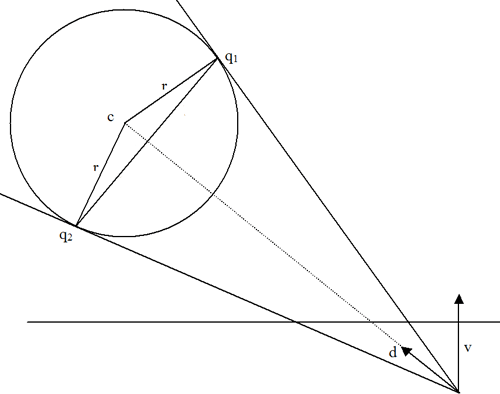
Donde cada elemento es:

• c es el centro de la esfera que contiene a la carga.
• r es el radio de la esfera que contiene a la carga.
• v es el vector director de la cámara de visión.
• d es el vector diferencia entre c y la posición de la cámara.
• q1 y q2 puntos tangenciales del cono con la esfera contenedora de la carga (estos son los puntos que nos darán la superfície de acotación).

Los datos conocidos son c, r, v y d; q1 y q2 se obtienen como:

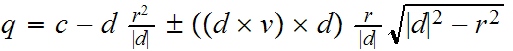
Basta entonces proyectar los puntos q1 y q2 obtenidos sobre el plano de la cámara para tener posicionada la elipse dentro del view-port. Claro que esos puntos por sí sólos no sirven. Como las elipses formadas por la proyección en el plano no serán muy pronunciadas por lo general aunque es lo más óptimo, podemos aproximar la acotación (trabajar sobre la elipse sería algo engorroso) por su círculo contenedor (ahora ya trabajamos en el view-port) cuyo centro está en (q1+q2)/2 y cuyo radio es |q1-q2|/2 y aunque lo más óptimo sería utilizar algún algoritmo de rellenado de círculos, podemos permitirnos volver a aproximar a su acotación por un rectángulo, quedándo la acotación de la carga dentro del view port como:

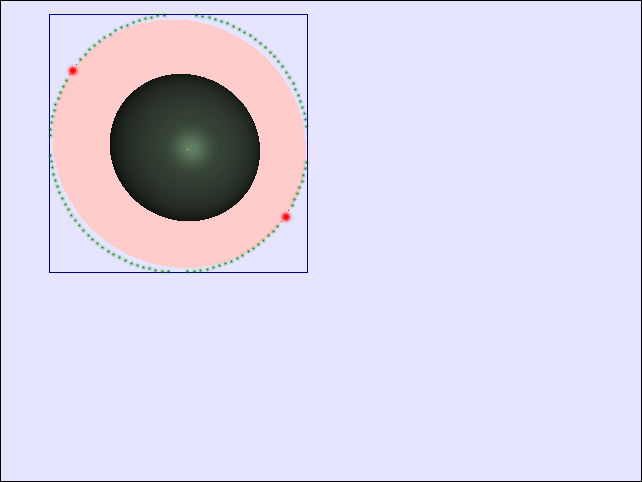
El resultado cuando el número n de cargas aumenta es evidente, pues el coste de organizar y calcular los cuadros de acotación es muy pequeño y lineal (sólo se debe calcular n veces para toda la imagen) y, gracias a esto, una carga sólo interviene en el proceso de cálculo cuando tiene muchas probabilidades de afectar a la superfície generada. O dicho de otra forma, el tiempo de generación de la imagen será proporcional no al número n de cargas en la escena, sino al número medio de cargas por píxel en el view-port que será muchísimo menor.

 descargar código fuente de Meta balls (2007).

---

Opinado el 09/07/09 09:13, valoración
    

---

Opinado el 05/05/10 10:50, valoración
    Jose Juan, sigues siendo un maestro.

---

Opinado el 07/06/11 21:34, valoración
    muy bueno