








 sobre 25 comentarios.
sobre 25 comentarios.
Comparación eficiente de imágenes
Tipos de comparación de imágenes

A grandes rasgos, podríamos clasificar la comparación (genérica) de imágenes de la siguiente forma:
- Imágenes con el mismo origen: en las que las imágenes comparadas son realmente la misma pero que ha sufrido algún tipo de alteración. Algunos ejemplos podrían ser:
- Se ha alterado el espacio de colores de las imágenes.
- Se ha recortado alguna de las imágenes.
- Se han modificado las proporciones de las imágenes.
- Se han modificado las resoluciones de las imágenes.
- etc...
- Imágenes con el mismo significado: en las que las imágenes comparadas no proceden del mismo origen e incluso su aparencia visual es completamente diferente. Por ejemplo, en estos casos es deseable que el comparador identifique un caballo visto de frente con un caballo visto de perfil. Ejemplos de los usos de este tipo de comparadores son:
- Revisión automática de piezas en cadenas de montaje y detección de fallos.
- Detección automática de personas en aeropuertos, estaciones de tren, etc...
- Reconocimiento automático de personas por la fisonomía de la cara.
- Reconocimiento automático de órganos internos del cuerpo humano.
- etc...
Como se ve, el segundo grupo de aplicaciones es mucho más disperso y mucho menos general, incluso en ocasiones no son imágenes las que se comparan, sino propiedades deseables dentro de una imagen. En estos casos se utilizan técnicas específicas en cada caso y optimizadas y calibradas para situaciones concretas.
El primer grupo presenta un tipo de problema mucho más concreto y sus aplicaciones mucho más limitadas. Lógicamente, la complejidad del primer grupo es muy inferior a las aplicaciones del segundo.
Objetivo propuesto
Como veremos, comparar dos imágenes para emitir un juicio en el sentido de saber si se trata de la misma imagen o no, es relativamente sencillo (dependiendo de las restricciones que impongamos a los parámetros de entrada). Sin embargo, nos proponemos poder establecer, dada una gran cantidad de imágenes, los grupos de imágenes equivalentes que existen dentro de él.
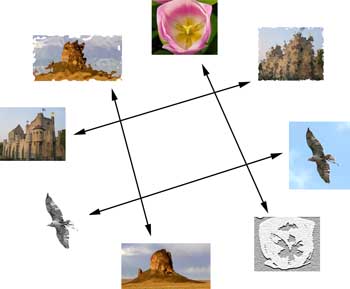
La aplicación principal es poder identificar las múltiples imágenes que se generan en nuestro repositorio personal, en el que muchas veces tenemos imágenes repetidas (porque las hemos guardado varias veces desde nuestra cámara) o muy similares (porque hemos hecho varias fotografías de la misma escena).
Comparando dos imágenes
Métrica
Una métrica es un objeto matemático que establece una relación entre dos elementos de un determinado conjunto. Informalmente, una métrica viene a ser como una distancia, es decir, las métricas generalizan el concepto de distancia a cualquier conjunto (al que se pueda definir una métrica, claro).
Así por ejemplo una métrica sobre el conjunto de todas las imágenes lo que establece es una distancia entre ellas.
El significado real de "medir" o tomar el valor de esa métrica para dos elementos cualesquiera es arbitrario y definido junto con la métrica aunque hablando de parecidos de imágenes, lo lógico es que nuestra métrica "mida" la distancia "en parecido" de ambas imágenes.
La ventaja de definir una métrica es que muchos de los principios y teoremas matemáticos serán válidos sobre el conjunto de las imágenes. Ésto es mucho más importante de lo que parece, puesto que definir una métrica sobre un conjunto nos dará una visión exacta de las propiedades de dicho conjunto, mientras que si definimos un objeto diferente a una métrica, desconocido para nosotros, no podemos estar seguros (hasta analizarlo profusamente) de las propiedades que posee. La desventaja es que es muy difícil encontrar una métrica que "funcione bien" para todas las transformaciones que queremos tratar.
Por ejemplo: si tenemos dos imágenes de la misma resolución (de Cols columnas y Fils filas) y mismo espacio de color (RGB con 3 componentes) entonces es n = 3 * Cols * Fils y podemos usar cualquier métrica válida para el espacio real n-dimensional como la siguiente:
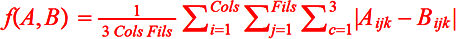
Es obvio que lo anterior es una métrica (puesto que lo es en Rn) y topológicamente hablando no necesitamos nada más para poder "alcanzar" todos los resquicios de nuestro espacio de imágenes, sin embargo, tiene un enorme problema y es que no se tiene en cuenta la información de proximidad entre puntos de la imagen es decir, hemos perdido esa información que lógicamente es necesaria, para demostrarlo, basta ver el siguiente par de imágenes de 4x4 píxeles.

Imágenes cuya distancia es la mayor posible, pero ¿son tan diferentes?
Ejemplos similares muestran lo complicado de definir una buena métrica. Y lo peor de todo es que no parece quedar claro qué propiedades son deseables en nuestra métrica, es decir, ¿qué es más importante (y en qué medida) a la hora de comparar dos imágenes?, o dicho de otra forma ¿qué las hace más parecidas o más diferentes?:
- ¿Diferencias en el color?.
- ¿Diferencias en el tamaño?.
- ¿En las proporciones?.
- ¿Rotación?.
- ¿Espectro?, ¿enfoque?, ¿sub-partes?, etc...
Parece claro que deberemos establecer restricciones al problema general de "comparar imágenes" si deseamos un método que podamos aplicar en la práctica.
Método simple de comparación
Si tan sólo deseamos comparar imágenes que sabemos son la misma salvo:
- Cualquier cambio de resolución.
- Cualquier cambio de escala.
- Pequeños recortes sobre alguno o varios márgenes.
- Ligeros cambios en el espectro de color.
- Ligeros cambios en la luminosidad y contraste.
- Ligeros cambios en la nitidez.
- Ligeros cambios en el nivel de ruido.
Entonces nos basta con la métrica anterior o alguna equivalente (todas las métricas definidas sobre el mismo conjunto son topológicamente equivalentes). La anterior tiene la ventaja de que nos dará un indicador de distancia entre 0 (muy parecidas) y 1 (muy diferentes). Y el procedimiento trivial consistiría en:
- Escalar ambas imágenes a una misma resolución prefijada (p.e. 50x50, 100x100, 200x200, ...).
- Aplicar el operador de la métrica definida.
Algunas adaptaciones adicionales que se pueden aplicar según interese son:
- Si no nos importa el color, descartarlo promediando las tres componentes en cada píxel de las dos imágenes.
- Si no nos importa el contraste, renormalizar las intensidades respecto la distribución.
Lógicamente la resolución "reducida" a la que se compararán las imágenes dependerá del tipo de precisión que se desea y las imágenes que se van a comparar. Es decir, si vamos a comparar puestas de sol y utilizamos una resolución muy pequeña, prácticamente todas las puestas de sol van a resultar ser la misma. Si por el contrario nos interesan patrones muy generales (por ejemplo para formar mosaicos), utilizar resoluciones muy grandes hará que todas las imágenes sean diferentes. En general 30x30 es una resolución lo suficientemente alta como para diferenciar ciertos detalles y lo suficientemente pequeña como para poderse indexar en una base de datos o mantenerla cacheada en memoria (algo muy importante si se desean comparar grandes cantidades de imágenes).
La imagen reducida pasaría a ser un pequeño resumen o "firma" de cada imagen.
Si tomamos la métrica anterior y analizamos un buen número de imágenes (unas 5500), podemos ver que tal se comporta dicha métrica a la hora de comparar unas con otras:
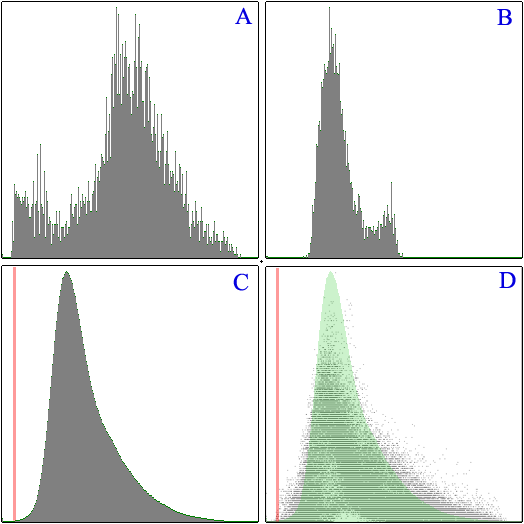
Cada una de las cuatro imágenes, representa la densidad del valor de comparación obtenido de una imagen con el resto. Cuanto más a la izquierda más parecidas son, cuanto más a la derecha menos parecidas son (respecto de la métrica usada, claro) y los valores de las gráficas nos indica el número de esas otras imágenes con ese índice de parecido.
La distribución A corresponde con una imagen cuyas comparaciones con otras imágenes resulta en tener bastantes que se le parecen y también bastantes que no se le parecen. Este tipo de imágenes serían las más fáciles de clasificar puesto que podremos encontrar grupos amplios de imágenes, es decir con "unos cuantos" grupos, tendremos clasificadas todas las imágenes.
La distribución B corresponde con una imagen cuyas comparaciones están muy centradas (tienen poca dispersión) y curiosamente ninguna se le parece bastante y ninguna se le diferencia mucho. Este tipo de imágenes serían las más difíciles de clasificar puesto que no se parece a ninguna otra imagen y, a priori, existirán tantos grupos como imágenes (puesto que no tienen parecido).
Si obtenemos un promedio de todas las gráficas generadas por todas las imágenes tenemos la distribución C que nos da una idea muy global del comportamiento de las comparativas pero muy engañoso. Para ver mejor cómo se comportan en general todas las distribuciones es mejor trazar la densidad directamente como en la gráfica D (a la que se le ha superpuesto en verde la gráfica A).
¿Qué nos indican estas distribuciones?, pues que ciertas imágenes serán muy parecidas al resto y otras muy diferentes, es decir, que nuestra métrica hace que aquellas imágenes con una distribución (en los colores) pequeña sean similares a aquellas imágenes cuya media coincide.
¿Tiene solución?, hasta cierto punto, será mejor utilizar una métrica como la distancia euclídea pues magnificará el factor (al ser un cuadrado en lugar de una diferencia) y rápidamente desestimará imágenes con píxeles más diferentes. Es decir, es mejor utilizar la métrica euclídea que la del valor absoluto.
Método exhaustivo de comparación
Casi en la misma linea pero generalizando el tipo de comparaciones, se podría almacenar no sólo un representante de cada imagen, sino todo un subconjunto jerarquizado de subimágenes. De esta forma, podríamos utilizar el mismo esquema para encontrar imágenes dentro de otras imágenes o bien trozos de imagen que son intersección de otras imágenes.
El procedimiento es sencillo, pero el conjunto de "firmas" que se generarán para cada imagen se dispara puesto que no sólo basta con dividir la imagen en celdas, sino que deben tomarse "firmas" de diferentes tamaños y para cada tamaño generar "firmas" con una única unidad de desplazamiento (y no sólo la cuadrícula del tamaño dado), por lo que será muy importante mejorar el algoritmo para comparar grandes cantidades de "firmas".

Cada sub-rectángulo de cada imagen es susceptible de ser "firmado"
Por ejemplo, supongamos que establecemos una "granularidad" de hasta 32x32 divisiones de la imagen. En ese caso, de primer nivel (tamaño 32x32) sólo tenemos una imagen (la original), de tamaño 31x31 tenemos 4, de tamaño 30x30 tenemos 9, etc... Todas estas firmas deben tenerse en cuenta (se suman) por tanto y, en general, para una subdivisión inicial de NxN celdas, tendremos un total de firmas de
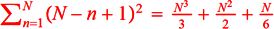
Pero es que además, si queremos tener en cuenta cambios en la proporción de las imágenes al ser "troceadas" (como por ejemplo la imagen que encabeza este artículo) debemos multiplicar (más o menos) por el número de proporciones que deseemos revisar.
En fin, que el procedimiento no es muy complicado, pero el número de imágenes de las que deberemos generar firma se dispara, por ejemplo, para un nivel razonable de partición de 16x16 celdas, cada imagen generaría ¡1496 firmas!.
Así y todo, el método es practicable aun cuando tengamos que procesar millones de imágenes puesto que las firmas sólo dependen de cada imagen y además el número de firmas a generar por imagen está prefijado. En el caso anterior de 16x16 niveles de subdivisión máxima, una firma de 30x30 píxeles (monocromo) y teniendo que procesar la barbaridad de 10 millones de imágenes, "sólo" tendríamos una base de datos de menos de 13 Gbytes.
Comparando miles o millones de imágenes
Comparar dos imágenes con firmas de NxN supone realizar 3 N2 operaciones (para cada píxel de la firma: diferencia de componente, valor absoluto y sumar al total), pero el problema es que si tenemos muchas imágenes (digamos M), el método "bruto" de compararlas todas con todas requeriría M2/2-M/2 comparaciones, dicho de otra forma, si tenemos "sólo" 1 millón de firmas (unas 700 imágenes), tendremos que realizar ¡medio billón de comparaciones!, en el mejor de los casos serían (con firmas de 30x30) un total de ¡125 horas! en un procesador a 3GHz. A todas luces no podemos ser tan brutos.
Jerarquía de "similitudes"
Podríamos establecer estructuras jerarquicas que relacionen las diferentes firmas. Una forma es agrupar las firmas por "similitud", en el sentido de que si la firma A se parece a la firma B y la firma B se parece a la firma C, podríamos deducir que la firma C se parece a la firma A. Ésto lo podemos asegurar porque se trata precisamente de la propiedad triangular que nuestra métrica cumple y queda patente la importancia de definir la métrica formalmente.
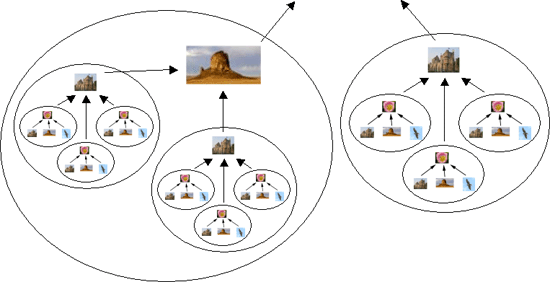
Este tipo de agrupaciones reducirá enormemente el número de comparaciones que deberemos hacer pasando de un desastroso coste O(n2) a un fantástico O(log n). La pega podría ser que la programación es más elaborada (y añadir o eliminar firmas requiere mucho más trabajo) y adecuada sólo para un entorno productivo (y no para un entorno de "probatinas" como el mío).
Un problema importante si se opta por este esquema es que como se vió anteriormente, no existe un único factor de comparación por el que se pueda comparar y no todas las imágenes son adecuadas para hacer de "claves de grupo" puesto que generarán grupos más o menos grandes de similitud. Ésto se debe a que la métrica obtiene la distancia sobre un elevado número de dimensiones y por tanto la "cercanía" de las imágenes se "reparte" sobre todas las dimensiones. En general, convendría tomar imágenes (para las "claves de grupo") con una distribución ni muy pequeña (pues demasiadas imágenes serían similares a ésta) ni muy grandes (pues muy pocas imágenes serían similares a ésta).
Indexación de componentes de firma
Si metemos todas nuestras firmas en una base de datos, nos podemos aprovechar de los algorítmos de indexación.
Indexar directamente los NxN componentes de la firma no nos servirá de mucho, y la única forma de poder hacerlo es crear un índice para cada componente (¡NxN índices!) por tanto la pega en este caso es que el número de índices para la tabla se dispara.
Si nuestro motor de base de datos no admite tantos índices podemos normalizar la tabla y, en lugar de crear la tabla como:
Podemos crearla como:
En cuyo caso, en lugar de NxN índices sólo tendríamos uno. Pero ojo, no creas que hemos mejorado mucho el problema de índices, de hecho, probablemente sea menos eficiente (el problema de los índices reside en que el motor debe revisarlos para cada inserción, actualización o eliminación de registros).
Bien, en cualquier caso, la forma adecuada de comparar las imágenes pasa por realizar consultas del estilo de "imágenes con al menos X componentes con un parecido mayor de K" y otras similares.
Indexación de propiedades globales
Otra forma de evitar tener que hacer muchas comparaciones es buscar propiedades generales que admitan un orden total y que discrimen en cierta medida el parecido de las imágenes. Es importante que las propieades admitan un orden, puesto que en otro caso no podrán indexarse adecuadamente.
Entonces lo que se desea son propiedades globales que aporten información de similtud. La media y desviación estandar podrían ser buenos indicadores aunque no serían capaces de discernir situaciones como cambios importantes de tonalidad, brillo, contraste, etc... (por ejemplo, la misma imágen pero más aclarada u oscurecida).
Existen multitud de indicadores que pueden tenerse en cuenta (mínimo, máximo, media, desviación, gradientes, etc...) sin embargo elegir uno bueno dependerá mucho del tipo de imágenes de que se trate: si son de motivos muy diferentes, una simple media nos aportará mucha información pero si son del mismo motivo (por ejemplo todo puestas de sol) trabajar sólo con la media no nos aportará grandes cambios.
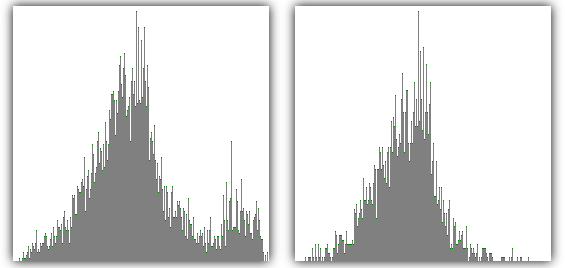
Comparación de la distribución de la media
Izquierda imágenes de diferentes motivos.
Derecha imágenes de motivos relacionados.
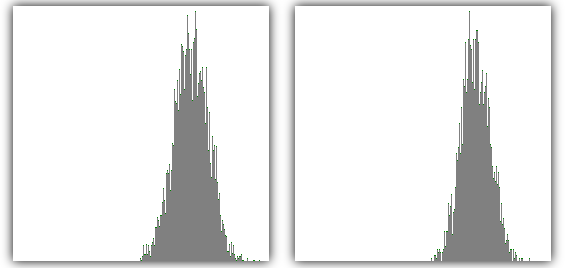
Comparación de la distribución de la desviación estandar
Izquierda imágenes de diferentes motivos.
Derecha imágenes de motivos relacionados.
Resúmenes de firmas
Si nos fijamos bien, al comparar las firmas estamos comparando el promedio de múltiples zonas en cada imagen. Es decir, puede que esas zonas resumidas sean idénticas y sin embargo las zonas "sin resumir" sean completamente diferentes. ¡Pero es que es realmente lo que queremos!, claro, tenemos el ejemplo de las imágenes "de ajedrez" anteriores. El caso extremo que hemos visto es directamente hacer el promedio de toda la imagen pero ésto, sabemos que es extremo cuando deseamos discriminar imágenes del mismo motivo (por ejemplo todo puestas de sol). Sin embargo, siempre tenemos el recurso de hacer comparaciones intermedias en el sentido de que comparar la media requiere comparar un único valor, comparar una firma de 2x2 píxeles sólo 4 valores, una firma de 3x3 sólo 9 valores y así sucesivamente. Si lo comparamos con el coste de contrastar las firmas de 30x30 o 60x60 píxeles, éstas últimas suponen ¡3600 operaciones!.
El resultado obvio es que podemos hacer comparaciones jerárquicas descartando directamente el resultado mientras podamos asegurar que es lo suficientemente diferente (aunque no podamos asegurar que es suficientemente parecida) puesto que una comparación más resumida nunca nos dará un resultado mejor que una comparación menos resumida.
El esquema sería:
- Comparamos la media, ¿es muy diferente? pues descartamos.
- Comparamos una mini-firma, ¿es muy diferente? pues descartamos.
- ...
- Comparamos la firma y devolvemos parecido.
Dicho de otra forma, para saber que dos imágenes son muy diferentes nos basta con información muy grosea y general y sólo cuando tenemos dudas aumentamos la precisión del análisis. Vuelve a quedar patente la importancia de la formalización de la métrica puesto que fácilmente puede verse que la distancia obtenida es monótona no creciente cuando la precisión de las firmas crece (informalmente quiere decir que si una firma nos da una distancia, aunque mejoremos la precisión de la firma, la distancia nunca aumentará, en todo caso disminuira), de ahí que podamos afirmar lo anterior (y lo siguiente).
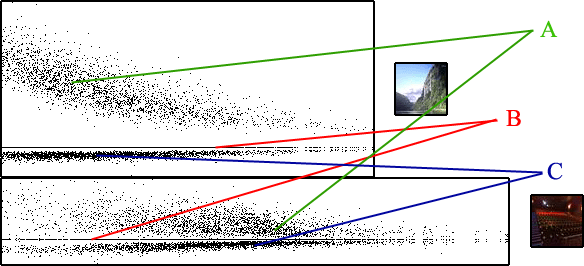
Se muestran las gráficas comparativas de los resultados de comparar todas las imágenes con las dos imágenes que se ven.
En cada gráfica se comparan tres valores obtenidos como:
- c1 la métrica con una única componente (vamos, el color medio). Una única operación.
- c2 la métrica con una "minifirma" de 8x8. 16 operaciones.
- c3 la métrica con una firma de 32x32. 1024 operaciones.
El significado de los puntos de las gráficas es el siguiente:
- Puntos B, son el eje horizontal y representan el punto que resulta de hacer la comparación sólo con la media (es decir, el valor c1). Los puntos más a la izquierda indican imágenes cuya media coincide con la analizada y los puntos más a la derecha indican imágenes cuya media se diferencia mucho de la analizada.
- Puntos A, es, sobre el mismo punto B, el aumento de precisión respecto de la media al utilizar la minifirma (es decir, es el valor c2 - c1).
- Puntos C, es, bajo el mismo punto B, el aumento de precisión conseguido con la firma completa respecto de la minifirma (es decir, es el valor c3 - c2).
Conclusiones:
- Si el valor medio es suficientemente diferente, está claro que podremos deducir que las imágenes son diferentes. Ésto es utilísimo, puesto que podemos indexarlo y discriminar rápidamente la mayoría de las imágenes (por ejemplo con una sencilla búsqueda dicotómica sobre las medias ordenadas).
- Una minifirma, aun cuando posee mucha menos información, ya nos arroja una conclusión "casi" definitiva, obteniendose una mejora mucho menor con la firma global.
- Utilizar múltiples firmas o firmas con "grandes" resoluciones (mayores de 10) sólo son útiles si queremos aproximación de motivos (por ejemplo para hacer mosaicos) y utilizar más de dos firmas (firma y minifirma) sólo parece adecuado cuando el número de imágenes a procesar sea realmente extraordinario (del orden de miles de millones).
Conclusiones
Realizar comparaciones de composición de imágenes (para hacer mosaicos o reemplazar motivos, emoticonos, etc...) o buscar imágenes parecidas es un problema que puede resolverse de forma muy eficiente (tanto en memoria como en tiempo) de forma sencilla aun cuando el número de ellas sea muy elevado.
Comparador de imágenes
Dejamos para el artículo Comparación eficiente de imágenes II el aprovechamiento efectivo de todas estas conclusiones para implementar una aplicación que realiza las búsquedas de imágenes de forma indexada.
Opinado el 21/06/10 03:02, valoración










Muy buen post, quizas un poco "poco riguroso" pero muy bueno como un post divulgativo y amplio.
Opinado el 29/06/10 04:03, valoración










Felicidades, y gracias por compartir tus conocimientos
Opinado el 18/09/10 20:30, valoración










Muy buen aporte. Te agradecer?que incluyeras algo de bibliograf?o que me enviaras un correo con ella a srivader@gmail.com Gracias
Opinado el 07/11/10 18:32, valoración










Interesante articulo, me he quedado con ganas de esa segunda parte. Como no se si usted vera este comentario, le he enviado un e-mail a la dirección que figura en el pie de pagina.
Opinado el 23/03/11 05:36, valoración










hola, genial explicacion entendi todo y eso que no estoy muy entrado en el tema, pero no veo por ninguna parte el articulo "Comparacion eficiente de imagenes II", supongo que no está listo, pero me interesaría muchisimo verlo cuando lo esté, no se si sea mucha molestia si me pudieras avisar cuando lo tengas listo o si abandonaste el proyecto, podrías decirme a mcf_hh@hotmail.com y otra vez muy buen trabajo!
Opinado el 15/06/11 23:22, valoración










Muy interesante. Te felicito
Opinado el 19/12/11 20:48, valoración










necesito contactarlo rmorrell@datasecuritys.com
Opinado el 26/08/12 02:58, valoración










muy buenaa
Opinado el 03/12/12 23:25, valoración










MUY BUENO E INTERSANTE
Opinado el 17/01/13 20:15, valoración










esta muy buena bro gracias me has salvado
Opinado el 24/01/13 16:57, valoración










y si muy bueno
Opinado el 04/04/13 13:53, valoración










Muy bueno, excelente
Opinado el 04/05/13 04:29, valoración










muy bueno elpost,este programa para rostros.
Opinado el 25/07/13 14:49, valoración










MUY BUENO, PARA MI OPORTUNO, Y SALVA A ALGUIEN..
Opinado el 29/09/13 21:28, valoración










salva dos.- Suprim,e el ojimetro
Opinado el 17/10/13 14:11, valoración










muy malo esta es publicidad engañosa
Opinado el 13/04/14 14:40, valoración










Exelnte muy amplie y explicativo gracias men
Opinado el 06/03/15 07:05, valoración










Excelente!!!. Muchas gracias
Opinado el 21/01/16 21:59, valoración










Opinado el 21/08/16 05:31, valoración










Perfecto. Algún código en C? arathburgos@gmail.com
Opinado el 03/05/18 20:37, valoración










bueno bueno
Opinado el 21/12/18 16:02, valoración










Opinado el 20/02/19 16:50, valoración










Opinado el 09/04/19 13:52, valoración










dennis.vargas1803@gmail.com como lo programo
Opinado el 26/06/20 17:16, valoración




















 Comparación eficiente de imágenes
Comparación eficiente de imágenes Línea sólida
Línea sólida Meta balls
Meta balls Radiosidad / Montecarlo
Radiosidad / Montecarlo Captura cara 3D
Captura cara 3D Trazador de rayos
Trazador de rayos