Línea sólida

Existen varios algoritmos para dibujar líneas (Bresenham, Xiaolin Wu y otros), sin embargo en algunas aplicaciones se debe seguir la trayectoria de una línea con otros fines que el de realizar un trazado.

¿Qué esferas de entre todas intersectan con el vector?, el algoritmo ingénuo es aquel que revisa la intersección del vector con cada una de las esferas, por tanto, si debemos realizar el cálculo para n vectores con m esferas, tendremos que calcular n · m intersecciones, ¿te parecen pocas?, si queremos renderizar una imagen a una modesta resolución de 1.024x768 píxeles (786.432 vectores) y tenemos 1 millón de esferas (por ejemplo simulando un líquido) son 786.432.000.000 intersecciones a 15 operaciones (son alguna más y entre ellas una hermosa raíz cuadrada...) nos da un total de ¡12.000 billones de operaciones! todo un derroche (en un procesador a 2GHz aproximadamente 1 hora y media). Y esto aunque sólo nos interese la primera intersección más próxima al orígen del vector. El número de intersecciones depende del número total de esferas.

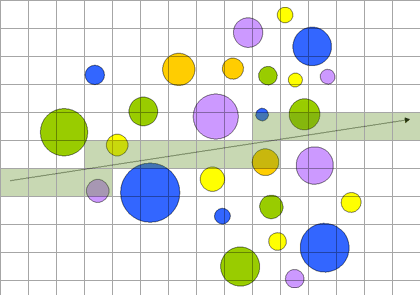
Si enrrejamos el espacio en el que se encuentran las esferas, sólo deberemos precalcular una única vez y para cada esfera con qué celdas posee intersección no nula y posteriormente para cada cada vector si cada celda tiene una densidad de d esferas y el vector una longitud media de l de d · l intersecciones cada vector. Pero es que además, si nos interesa la primera intersección ocurre que, si d aumenta significa que hay muchas esferas y por tanto la probabilidad de colisión es alta y por tanto l será pequeño. Si por el contrario d es pequeño la probabilidad de que no haya esferas en las celdas es pequeño. Poniendo una cota superior que la densidad sea 1 y que aun así l sea la mitad de la diagonal de un cubo de 1000 esferas de lado ¡1000 veces más que antes! el número de intersecciones por vector serían menos de 1250 (la diagonal del cubo) con un coste total en operaciones de 20.643.840.000 y un tiempo estimado de ¡sólo 10 segundos! (aunque nos cueste preprocesar las esferas, sólo se hace una vez).

¿Cómo sabemos sobre qué celdas transcurre el segmento?

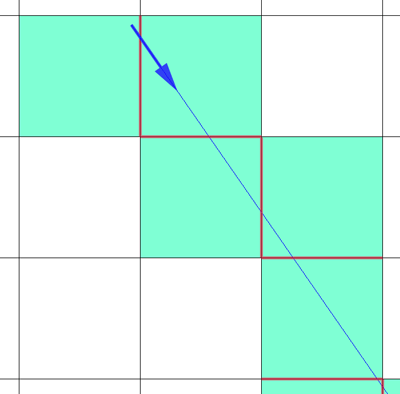
Si nos fijamos en cualquier vector que tracemos dentro de una cuadrícula, si partimos desde una celda:

• Deberemos pasar a la siguiente horizontal si intersecta con la arista vertical.
• Deberemos pasar a la siguiente vertical si intersecta con la arista horizontal.

Realmente más simple no podría ser, ahora bien, ésto debe concretarse, para ello y sin pérdida de generalidad definimos los elementos siguientes:

• Posición origen del segmento O = ( Ox, Oy )
• Vector director (normalizado) del segmento D = ( Dx, Dy )
• Todas las celdas tienen el mismo lado que alto y de medida 1
• El número (entero) de celdas definidos en la rejilla viene dado por N = ( Nx, Ny )
• Las celdas están enumeradas por su posición central que será entera ( 0, 0 ), ( 1, 0 ), ( 2, 0 ), ..., ( Nx - 1, 0 ), ( 0, 1 ), ( 1, 1 ), ( 2, 1 ), ..., ( Nx - 1, 1 ), ..., ( 0, Ny - 1 ), ( 1, Ny - 1 ), ( 2, Ny - 1 ), ..., ( Nx - 1, Ny - 1 )
• La posición (global) de la menor de las celdas (aquella más próxima al origen de coordenadas) en su centro es C = ( Cx, Cy )

Así las cosas, podemos sacar algunas relaciones:

• Las dimensiones de la rejilla son ( Nx, Ny )
• La esquina inferior de la rejilla es Ei = ( Cx - ¹/₂, Cy - ¹/₂ )
• La esquina superior de la rejilla es Es = ( Cx + Nx - ¹/₂, Cy + Ny - ¹/₂ )

Y como lo normal será querer especificar los vértices que delimitan la rejilla y el número de divisiones que se desean, si tenemos Qi = ( Qix, Qiy ) la esquina inferior, Qs = ( Qsx, Qsy ) la esquina superior y Sx el número de divisiones sobre el eje x, sólo tenemos que establecer las transformaciones entre los sistemas (podríamos independizar las divisiones para cada eje, pero no merece la pena el esfuerzo, pues rara vez la distribución de los objetos dependerá de cada eje):

• El sistema local es paralelo al global, sólo que escalado en un factor de escala = ^{( Qsx - Qix )} / _Nx.
• El orígen de coordenadas del sistema local está en C = Qi + escala * ( ¹/₂, ¹/₂ ).
• Un punto se transforma mediante global = C + local * escala.

Ahora, lo siguiente que debemos hacer es mirar a ver si nuestro segmento colisiona con la rejilla, para ésto, podemos usar un algoritmo de recorte de líneas como el de Liang-Barsky que, aunque para nuestro caso se podría optimizar (al menos en media) no merece la pena, ya que si vamos a usar un número masivo de sub-rejillas entonces merecerá la pena meterlas todas en una super-rejilla y entonces siempre el vector se inicia dentro cada rejilla (por lo que no hace falta el recorte).

El algoritmo de Liang-Barsky es muy fácil de implementar, éste que ves, ya está modificado para recorte en 3 dimensiones:

Nos queda aún implementar la idea concreta del recorrido sobre celdas que comentamos arriba del todo, para esto debemos realizar un par de optimizaciones importantes:

• En cada iteración debemos evitar realizar multiplicaciones o divisiones.
• En cada iteración debemos evitar realizar conversiones de int a double y viceversa.

Entonces, recordamos que debemos pasar a la celda adyacente (a aquella en la que estamos) sobre la arista (o plano) que primera intersectamos (ver imagen de más arriba) y obviamente será sobre la coordenada cuyo parámetro (de la recta) sea menor en la frontera de la celda. Ésto además, podemos hacerlo con independencia del número de coordenadas que tenga nuestro sistema ( 2D, 3D, 4D, ... ). Por tanto, directamente con los comentarios en el código debe ser suficiente para entender el cálculo de los parámetros para ir pasando de semiplano a semiplano en cada coordenada:

La zona roja es la que se evalúa en cada iteración cada vez que se pasa de celda a celda y, además, sólo para el eje de paso, como vemos, el coste es muy pequeño, y pueden evaluarse miles de celdas en el tiempo que costaría evaluar una única intersección en otro tipo de objetos (una esfera, una superfície Bezier, una metabola, ...).

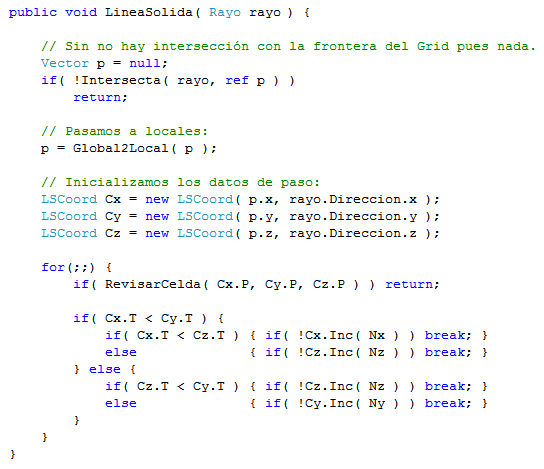
Poco o nada hay que decir del código anterior:

• Si no está dentro del grid o no intersecta, no hay nada que hacer.
• Si está dentro del grid, entonces pasamos a coordenadas locales.
• Para cada componente calculamos los parámetros de paso.
• Iteraremos ininterrumpidamente:
  • Hasta que la celda en la que estemos colisione.
  • O bien si al pasar a la siguiente celda, ésta queda fuera del grid.

Para ver los resultados, puedes compilar este proyecto en C# (MS Visual Studio 2005).

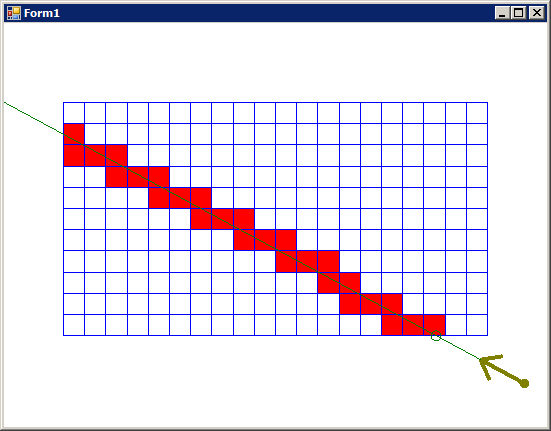
 descargar código fuente de Línea sólida.

---

Opinado el 17/05/10 03:24, valoración
    

---

Opinado el 08/03/11 12:45, valoración
    

---

Opinado el 16/04/13 02:35, valoración