Terreno 3D

Las aplicaciones gráficas en tiempo real se basan principalmente (aunque existen múltiples técnicas que no) en representar las geometrías (las formas que tienen los objetos a manejar) mediante triángulos. Si alguien ha visto el parque Güel de Barcelona, se habrá fijado que las formas redondeadas de las paredes, columnas y chimeneas se recubren con un montón de pequeños trocitos de ladrillo o valdosa. En informática gráfica, esas valdositas se consiguen con pequeños triángulos.

Para que los objetos así representados tengan la mayor calidad posible, una de las formas (no la única) es aumentar el número de triángulos, pero ésto requiere que los ordenadores tengan que hacer cálculos con un número mayor de triángulos y por tanto van mas lentos cuantos más triángulos se usan.

En casi todas las aplicaciones, los objetos NO siempre es necesario que esten representados con gran calidad (tengan muchos triángulos) pues si por ejemplo están a bastante distancia de la cámara, el objeto se ve pequeñito y de nada sirve utilizar muchos triángulos.

Una de las aplicaciones que más se beneficia de esta estrategia (utilizar sólo los triángulos necesarios respecto la calidad que se necesita) son aquellas que modelan terrenos.

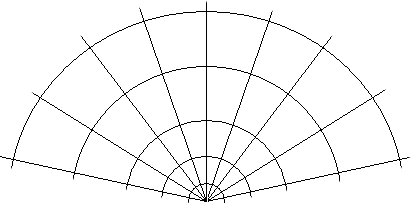
Existen muchos algoritmos para dibujar terrenos de forma adaptada, yo aquí me aprovecho de una técnica de barrido muy rápida ray-casting realizándola de forma radial, junto con un incremento progresivo del avance del rayo de testeo, de forma que se genera en cada frame (imagen de una película) una malla de triángulos en la que las zonas más próximas a la cámara son las que poseen triángulos más pequeños, mientras que las más alejadas, más grandes.

Para darle un poco más de "intríngulis" a la cosa, situe unos cuantos avatars (entidades con vida propia) a los que se les puede disparar.

Por lo demás, los avatars se modelaron con 3DMax exportándolos a formato de texto ASE y el mapa que ves es un "mar" de Marte tomado de la NASA.

 descargar código fuente y ejecutable de Terreno 3D.

---

Opinado el 05/08/10 23:26, valoración
    esta chido

---

Opinado el 09/02/17 11:55, valoración
    eres dios